论文一时爽，复现火葬场

2020年04月18日 3k 字大概 13 分钟

身如钢铁，心若琉璃

前言

随着技术门槛的降低以及在如今机器学习、深度学习变得日渐大白菜的大背景下。人人都能够上手训练神经网络调试参数，私以为没有数学基础已经相应的编程功底很难再实现自己的无可替代性，故开一贴，记录思考，寻求变革！

实现步骤

环境准备：
- 硬件篇:性能拉满，模型吃灰，不如去打游戏！
- 软件篇：总有de不完的BUG
分析模型
- 数学原理：谁会啊~你会嘛，我不会
- 模型实现：Ctrl+C+V：这我熟悉
模型实现
- 处理数据：PyTorch加载自己的数据集
- 模型搭建：？？？
- 模型训练：？？？
- 模型测试：？？？

环境准备

硬件设备：RTX30601、TITAN Xp2
软件：RTX3060:Nvidia462.30+CUDA11.1+cudnn8.0.1+pytorch1.8
TITAN Xp:Nvidia460.72+CUDA10.7+cudnn7.0.1+pytorch1.7
2021年下半年显卡选购攻略

分析模型

识别手写数字，除了使用传统的贝叶斯概率模型，感知机或者支持向量机做分类意外，使用图像的方法越来越主流，尤其是再imageNet，已经超越了人类达到了惊人的99%！

数学原理

LeNet-5出自论文Gradient-Based Learning Applied to Document Recognition，是一种用于手写体字符识别的非常高效的卷积神经网络。
PS：数学上的卷积操作自行参考网络与信号系统教科书（PS：如果没有卷积操作对数值特征的名感性，也就没有后来的图像处理什么事情了）

激活函数操作，选用，以及意义

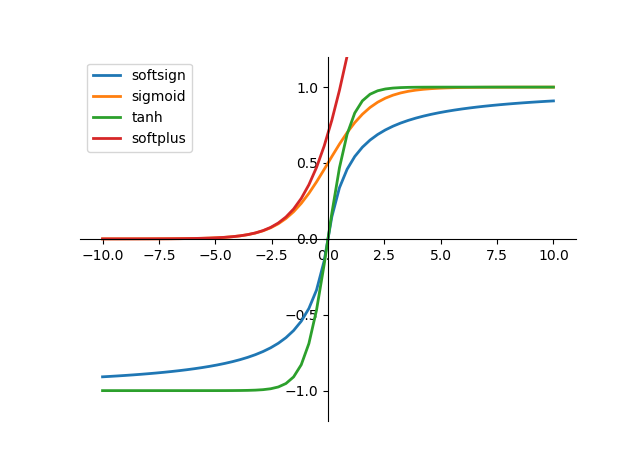
激活函数本质上是为了增强网络对非线性参数的拟合能力
激活函数是来向神经网络中引入非线性因素的，通过激活函数，神经网络就可以拟合各种曲线。如果不用激励函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合。如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。
激活函数主要有两大类：Relu与sigmoid
sigmoid：sigmoid是使用范围最广的一类激活函数，具有指数的形状，它在物理意义上最为接近神经元。sigmoid的输出是（0，1），具有很好的性质，可以被表示做概率或者用于输入的归一化等等。
tanh: tanh也是一种非常常见的激活函数，与sigmoid相比，它的输出均值为0，这使得它的收敛速度要比sigmoid快，减少了迭代更新的次数。
Relu：ReLU是针对sigmoid和tanh的饱和性二提出的新的激活函数。从上图中可以很容易的看到，当x>0的时候，不存在饱和问题，所以ReLU能够在 x>0 的时候保持梯度不衰减，从而缓解梯度消失的问题。这让我们可以以有监督的方式训练深度神经网络，而无需依赖无监督的逐层训练。然而，随着训练的推进，部分输入会落入硬饱和区（即 x<0 的区域），导致权重无法更新，这种现象称为“神经元死亡”。
LeNet5参数详解（麻雀虽小，五脏俱全)
数据类型：有Mnist数据集图像为3232
1. 先把图像的特征卷积出来（卷积核过大过小都不好，过大容易丢失细节信息，过小容易过拟合以及降低模型训练速度，一般选用样本大小的五分之一较为适宜），这里采用55，故原特征降为（32-5+1）2828
2. 激活函数使用（）
3. 池化过滤掉一些不重要的特征，消除弱化扰动，提高对特征识别的鲁棒性（池化操作还有很好的特征降维、防止过拟合的作用）采用22,故得1414
4. 继续重复卷积得1010（14-5+1）,这里通过特征图的组合运算得到了16各特征图。第一次池化之后是第二次卷积，第二次卷积的输出是C3，16个10x10的特征图，卷积核大小是 55. 我们知道S2 有6个 14*14 的特征图，怎么从6 个特征图得到 16个特征图了？这里是通过对S2 的特征图特殊组合计算得到的16个特征图。具体如下：

5.继续下采样池化
6.全连接后输出

模型实现

数据处理dataset.py

1 2	`import torchvision torchvision.datasets.MNIST('./data', download=True)`

模型搭建model.py

#model.py
import torch
import torch.nn as nn
from torch.nn.modules import module
from torch.nn.modules.linear import Linear
'''

从图中可以看出，其输入32x32的灰度图像，由于MNIST数据集的图像为28x28，因此，我们将输入改为28x28，并依次计算每一层输出的特征图大小。其每一层参数大致如下：

输入层：输入大小28x28，通道数为1。注意：本层不算LeNet-5的网络结构，一般情况下不将输入层视为网络层次结构之一。

C1-卷积层：输入大小28x28，通道数为1；输出大小28x28，通道数为6；卷积核大小为5x5；步长为1；边缘补零为2；激活函数为ReLU。注意：为了提升卷积神经网络的效果，在每个卷积层后添加激活函数，本教程使用的激活函数为ReLU。

S2-池化层：输入大小28x28，通道数为6；输出大小14x14，通道数为6；池化核大小为2x2；步长为2；池化方式为最大池化。

C3-卷积层：输入大小14x14，通道数为6；输出大小10x10，通道数为16；卷积核大小为5x5；步长为1；边缘补零为0；激活函数为ReLU。

S4-池化层：输入大小10x10，通道数为16；输出大小5x5，通道数为16；池化核大小为2x2；步长为2；池化方式为最大池化。

C5-卷积层：输入大小5x5，通道数为16；输出大小1x1，通道数为120；卷积核大小为5x5；步长为1；边缘补零为0；激活函数为ReLU。注意：这层也可以看作全连接层，可以通过全连接的方法实现。

F6-全连接层：输入为120维向量；输出为84维向量；激活函数为ReLU。

OUTPUT-输出层：输入为84维向量；输出为10维向量。注意：该层也是全连接层，且不带激活函数。
'''

class LeNet(nn.Module):#定义模型，继承torch本身里的类型

    #初始化函数
    def __init__(self):
        super(LeNet,self).__init__()
        self.C1 = nn.Conv2d(in_channels=1,out_channels=6,kernel_size=5,stride=1,padding=2)
        """
        in_channels：输入的通道数

        out_channels：输出的通道数

        kernel_size：卷积核的大小。若卷积核是方形，则只需要一个整数边长；若不是方形，则需要输入一个元组表示高和宽

        stride：卷积核每次滑动的步长，默认为1

        padding：设置边缘补零的大小（也就是在输入特征图外围增加几圈0）

        dilation：控制卷积核之间的间距，默认为0；若使用空洞卷积则需要对该参数进行设置

        groups：控制输入和输出之间的连接，平时不常用，若使用分组卷积则需要设置该参数

        bias：是否设置偏置，默认为 True

        adding_mode：边缘补零模式，默认为”zeros“
        """

        self.R1 = nn.ReLU()
        self.S2 = nn.MaxPool2d(kernel_size=2,stride=2)
        self.C3 = nn.Conv2d(in_channels=6,out_channels=16,kernel_size=5,stride=1,padding=0)
        self.R2 = nn.ReLU()
        self.S4 = nn.MaxPool2d(kernel_size=2,stride=2)
        self.C5 = nn.Conv2d(in_channels=16,out_channels=120,kernel_size=5,stride=1,padding=0)
        self.R3 = nn.ReLU()
        self.F6 = nn.Linear(in_features=120,out_features=84)
        self.R4 = nn.ReLU()
        self.OUT = nn.Linear(84,10)

    #前向函数
    def forward(self,x):
        x = self.C1(x)
        x = self.R1(x)
        x = self.S2(x)
        x = self.C3(x)
        x = self.R2(x)
        x = self.S4(x)
        x = self.C5(x)
        x = self.R3(x)
        x = x.view(x.size(0), -1)#计算批大小。size，-1=120（自动计算）改变维度，四维转成二维，因为全连接层之接受二维张量输入
        print(x.size())
        x = self.F6(x)
        x = self.R4(x)
        x = self.OUT(x)
        return x

if __name__ == "__main__":
    model = LeNet()
    print(model)
    a = torch.randn(1,1,28,28)
    b = model(a)
    print(b.size())

模型训练train.py

import torch
import torchvision
import torch.nn as nn
import torch.utils.data as Data

from model import LeNet
model = LeNet()#导入模型

Epoch = 5
batch_size = 64
lr = 0.001

train_data = torchvision.datasets.MNIST(root='./data/', train=True, transform=torchvision.transforms.ToTensor(), download=False)#定义数据集

train_loader = Data.DataLoader(train_data, batch_size=batch_size, shuffle=True, num_workers=0, drop_last=True)#把数据喂给模型
'''
Data.DataLoader(dataset, batch_size, shuffle, sampler, batch_sampler, num_workers, collate_fn, pin_memory, drop_last, timeout, worker_init_fn, prefetch_factor, persistent_workers)
以下是其常用参数的介绍：

dataset：数据集，可以使用Data.DataSet类或者torchvision.datasets

batch_size：批大小，每次迭代送入模型的图像数量

shuffle：是否打乱数据集，默认为False

num_workers：使用的线程数，DataLoader支持多线程读取数据以提升效率，该值为0或1是使用单线程进行读取。一般情况下该值不要超过cpu的最大线程，如果使用GPU训练模型的话该值越大其显存占用也会越大，日常使用中需要根据电脑的配置进行调节。默认为0

pin_memory：是否使用锁页内存，可以理解为是否将数据集全部强制加载进内存，且不与虚拟内存进行交换，设为True的话可以使得模型的训练快一些，默认为False

drop_last：是否丢弃最后不足batch_size的数据。有时候，数据集并不能整除batch_size，最后一批图像的数量会小于batch_size，这个参数决定是否将这一批数据丢弃，默认为False
'''
#损失函数与优化器
loss_function = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
#启用梯度
torch.set_grad_enabled(True)
model.train()
#CUDA加速
device = torch.device("cuda:0" if torch.cuda.is_available() else "cuda:1" or "cpu")
print(device)
model.to(device)
'''
在pytorch中，神经网络的训练一般是分以下几个步骤进行的：

1) 获得DataLoader中的数据x和标签y

2) 将优化器的梯度清零

3) 将数据送入模型中获得预测的结果y_pred

4) 将标签和预测结果送入损失函数获得损失

5) 将损失值反向传播

6) 使用优化器对模型的参数进行更新

'''
for epoch in range(Epoch):#设置遍历数据集
    running_loss = 0.0
    acc = 0.0
    for step, data in enumerate(train_loader):#便利迭代
        x,y = data #1
        optimizer.zero_grad()#2
        y_pred = model(x.to(device,torch.float))#3
        loss = loss_function(y_pred,y.to(device,torch.long))#4
        loss.backward()#5
        running_loss += float(loss.data.cpu())
        pred = y_pred.argmax(dim=1)
        acc += (pred.data.cpu() == y.data).sum()
        optimizer.step()#6
        if step % 100 == 99:#训练进程可视化
            loss_avg = running_loss / (step + 1)
            acc_avg = float(acc / ((step + 1) * batch_size))
            print('Epoch', epoch + 1, ',step', step + 1, '| Loss_avg: %.4f' % loss_avg, '|Acc_avg:%.4f' % acc_avg)
#保存模型
torch.save(model,'./LeNet.pkl')

模型测试test.py

import torch
import torchvision
import torch.utils.data as Data

test_data = torchvision.datasets.MNIST(root='./data/', train=False, transform=torchvision.transforms.ToTensor(), download=False)#测试数据
test_loader = Data.DataLoader(test_data, batch_size=1, shuffle=False)

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

net = torch.load('./LeNet.pkl',map_location=torch.device(device))#模型

net.to(device)#放进CUDA

torch.set_grad_enabled(False)#关闭自动求导，不反梯度更新模型参数（测试）
net.eval()

length = test_data.data.size(0)#获取测试集合的大小
acc = 0.0
for i, data in enumerate(test_loader):#同训练，acc=正确/总样本
    x, y = data
    y_pred = net(x.to(device, torch.float))
    pred = y_pred.argmax(dim=1)
    acc += (pred.data.cpu() == y.data).sum()
    print('Predict:', int(pred.data.cpu()), '|Ground Truth:', int(y.data))

acc = (acc/length)*100
print('准确率：%.2f'%acc,'%')