No Game No Coding

2021年12月12日 22.6k 字大概 105 分钟

Coding Learning from 代码随想录/labuladong算法小抄

无游戏不编程

在我看来，编程这回事和我玩的大型战略游戏（星际，魔兽）没有太大的区别。从某种角度上讲：变量就是我生产的最小战斗单位，类似于一个个执行生产任务的工兵；函数无非就是为他们提供冲锋思路（没有返回值，过程中带来一些战果）、打造的武器装备（例如numpy转tensor）或者回炉重铸打造出更合适的单位（带返回值），类就是我设计好的作战集群，里面有各式各样的职阶和武装。我可以以剑圣为蓝本生成一个无敌的类，初始化属性数值拉满，技能隐身跳砍、火舞旋风移速快的同时伤害还可以爆炸~

Leetcode学习日历

安利这个神奇的网站
逻辑完美，细节精巧，代码AC
个人编程菜鸡速成打法步骤：

大致阅览某一类型题的基础知识，知道这是个什么东西即可
开始跟着这一类型刷题，总结思路，尝试写出这种思路的清晰伪代码
隔一段时间后（1~3天内为宜，因为对题的思路还有印象）重新看题回忆这部分伪代码，想不起来就找出之前的笔记，根据伪代码还原出AC的代码
归纳这一类体型和伪代码解题套路（为什么不是思路，因为只是有思路没有代码还原能力的锻炼在编程中是万万不可取的，是代码人的大忌，记伪代码的同时一般也会顺便记住代码还原的关键地方）
开始新循环或者刷新题稳固、拓展、归纳、梳理到自己的套路中来

数据结构基础

算法性能：时间复杂度与空间复杂度

时间复杂度是一个函数，它定性描述该算法的运行时间
空间复杂度是对一个算法在运行过程中占用内存空间大小的量度，记做$S(n)=O(f(n)$。空间复杂度(Space Complexity)记作S(n) 依然使用大O来表示。利用程序的空间复杂度，可以对程序运行中需要多少内存有个预先估计

数组

概念：连续内存空间上相同数据的集合：内存是挨着的，数据类型是相同的

基本知识：
1. 数组可以通过下标寻址，删除或者插入元素要对整个数组进行连续位移操作
2. 数组下标都是从0开始，而且在内存空间分配上是连续的
  二分查找问题

使用条件：在一个有序的数组里，直接用二分法判别相当于卡德一下就干掉了一半的数据，极为搞笑，类似于数学里的不断二分求函数在某一个区间上的极值点一样。PS:数组有序，并且无重复元素是前提，二分法不会写基本就是边界左右怎么选定没搞清楚，可以用闭区间，也可以用左闭又开等，具体考虑实际意义

经典的二分法寻值问题

class Solution(object):
    def search(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        left = 0
        right = len(nums)-1
        while left <= right: #此处规定区间左右界规则很重要，当二分到左右界会交叉时break，返回-1
            middel = (right + left) / 2 #这一步是我的代码
            #middel = ((right - left) // 2) + left #官方代码
            if nums[middel] == target:
                return middel
            #设想思路，此处num[middle]已经和target比较过了，所以下面再比较时可以将边界向左向右位移一位。
            if nums[middel] > target:
                right = middel - 1 #错因，没有搞清楚二分之后左右边界的选择问题，目标在左应该把右边界往中间偏左缩减一位
            else:
                left = middel + 1 #目标在右应该把左边界在中位数上往右走一位，确定合适的区间
        return -1

寻值求插入问题

class Solution(object):
def searchInsert(self, nums, target):
    """
    :type nums: List[int]
    :type target: int
    :rtype: int
    """
     #二分法找个数，没有就返回索引
    left = 0
    right = len(nums) - 1
    if target <= nums[left]:
        return 0
    if target > nums[right]:
        return right + 1
    while left <= right:
        print(left)
        print(right)
        mid = int((left + right) / 2)
        print(mid)
        if nums[mid] < target:
            #目标在右边
            left = mid + 1
        if nums[mid] > target:
            #目标在左边
            right = mid - 1
        if nums[mid] == target:
            return mid #寻找值情况，如果target在序列里，返回此时的mid
    # 如果target不在序列里，有什么数学/逻辑关系可以判明他的索引
    if target < nums[mid]:#看循环，当target不在序列里，循环最终会输出mid = left = right，所以判别target在mid的左右相对关系既可以找到其位置，当target小于num【mid】时，此时在mid处插入，
        return mid
    else: #如果target大了，那就在后一位插入，所以索引加1
        return mid + 1

OOOOXXXX类数组第一个错误X出现在哪的问题

class Solution:
def firstBadVersion(self, n):
    """
    :type n: int
    :rtype: int
    """
    #题意明说少调用，肯定排除了遍历，出了遍历还能找到查询的方法只有二分搜索了
    #可以转化为在[oooooXXXXXX]中查找第一个X，O,X类似于大小比较
    left = 0
    right = n
    print(isBadVersion(0))
    while left < right:
        mid = int((left + right) / 2) #特殊个例，单圈或者单叉的情况下怎么让循环也能判断出来，把左边虚拟成0版本，反正是X的话马上就会+1跳出循环，此时right是1，题意bad大于1很关键，如果bad可以等于0，但我的right任然会取到1，所以要另外加上无错误返回false的判别
        print(mid)
        if isBadVersion(mid):
            #检测到错误版本
            right = mid          #为什么这么写，因为题意要求的是第一个叉何时出现，所以最终值一定是取在right上的，判定时机就是当right取到target时，left会不断+1直到等于right，此时return
        if not isBadVersion(mid):
            #检测到非错误版本
            left = mid  + 1
    return right

元素移除问题

问题：给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并原地修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

方法：
- 双for循环：一个for遍历数组，一个for更新数组：一个for找到重复数，另一个for调整删去重复树
- 双指针法：快慢指针快速的遍历查找，慢指针不断按快指针参数调整数组，在目标值的时候快指针直接++跳过去，然后将后一位连接给慢指针（当快指针遇到目标值时，慢指针会停下）所以当快指针继续操作时会把目标后面的值衔接到慢指针后，达到删去目标元素的功能。

代码：

class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
        fast = slow = 0
        while fast < len(nums):
            if nums[fast] != val:
                #fast += 1
                nums[slow] = nums[fast]
                slow += 1
            fast += 1
                
        return slow

有序数组的平方问题

给你一个按非递减顺序排序的整数数组 nums，返回每个数字的平方组成的新数组，要求也按非递减顺序排序。排序此时最好不用内置函数sort
思路：

暴力排序：先计算后排序，时间复杂度大概是n+nlogn

双指针法：双指针的使用很巧妙的解决了计算和排序的问题，变计算边比较边排序，时间复杂度为n（只进行了一次从右到左的遍历排序）

class Solution {
public:
    vector<int> sortedSquares(vector<int>& A) {
        int k = A.size() - 1;
        vector<int> result(A.size(), 0);
        for (int i = 0, j = A.size() - 1; i <= j;) { // 注意这里要i <= j，因为最后要处理两个元素
            if (A[i] * A[i] < A[j] * A[j])  {
                result[k--] = A[j] * A[j];
                j--;
            }
            else {
                result[k--] = A[i] * A[i];
                i++;
            }
        }
        return result;
    }
};

pyothon解法：

class Solution:
    def sortedSquares(self, nums: List[int]) -> List[int]:
        l = len(nums)
        i,j,k = 0, l - 1, l - 1
        ans = [-1] * l
        print(ans)
        while i <= j:
            lm = nums[i] ** 2
            rm = nums[j] ** 2
            if lm >= rm:
                ans[k] = lm  
                k -= 1
                i += 1       
            else:
                ans[k] = rm
                k -= 1
                j -= 1
        return ans

长度最小的子数组问题

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的子数组，返回0。
滑动窗口法

class Solution: #此代码逻辑是通的，只不过逐个滑动放缩窗口效率比较低，应该采取双滑动
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        l = len(nums)
        i, j, k = 0, 0, 0
        t_lmin = 0
        lmin = l
        count = 0
        while i <= l - 1:
            while j <= l - 1: 
                count = count + nums[j]
                print(count)
                if count >= target: #满足大于的条件了，看是否是最短序列
                    t_lmim = j - i + 1 
                    #这一步之后其实可以用上conut -=nums[i]让左指针也跟着动
                    if t_lmim <= lmin: #满足目前是最小序列条件，更新
                        k = 1
                        lmin = t_lmim
                        break
                    else: #这个i下不满足最小序列，爬
                        break
                #不满足大于条件，右指针要开始向右移动扩大数组求值范围
                else:
                    j += 1
            i += 1 
            j = i
            count = 0
            if lmin == 0:
                return lmin
        if k == 1:
            return lmin
        else:
            return 0

class Solution: #最佳，此方法与我的方法相比更为简洁，我是逐个移动左指针然后求右，时间复杂度为（n+nlogn）这个方法是双移动指针，一直用某一个区间去适配，小了改大，大了改小，一直移动遍历完数组就可以了，不用重复多次循环计算输出。
    def minSubArrayLen(self, target: int, nums: List[int]) -> int:
        l = len(nums)
        i, j = 0, 0
        lmin = float("inf")
        count = 0
        for i in range(l):
            count += nums[i]
            while count >= target:
                lmin = min(lmin, i-j+1)
                count -= nums[j] # 左指针右移，值区间缩减
                j += 1
        if lmin == float("inf"):
            return 0
        else:
            return lmin

螺旋矩阵问题

给定一个正整数 n，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。
*:在这一道题要开始深入理解循环不变量原则，就是在循环使用的时候，要清楚什么变量是可以动的，什么是不可以动的，区间的大小，开闭情况都要考虑一下，不然就容易写出各种bug的死循环。

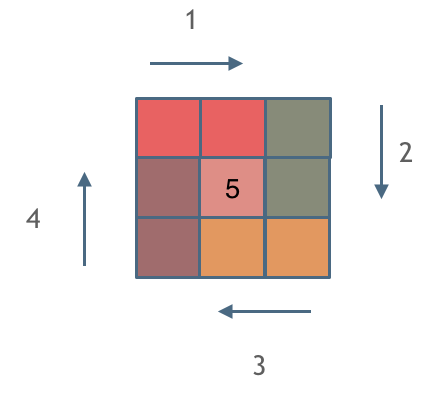
代码要逻辑自洽，过度依赖临时逻辑修修补补往往都是拆了东墙补西墙自讨苦吃
- 比如本题，既然是寻找螺旋数字特征，就应该依据螺旋走向的逻辑逐步往里一层一层循环遍历赋值
  而不是纯纯列出矩阵后边遍历边运算边赋值。下图可以看出，边界条件很多，如果不控制好逐层全覆盖的逻辑表达，则很难写出准确的代码。

逻辑矩阵也有许多变体,比如有一些不规则的矩阵，有可能是遍历，有可能也是填充，但本质都离不开确定好四条边后进行操作

class Solution:
    def generateMatrix(self, n: int) -> List[List[int]]:
        #定义一个大小为n*n的二维数组
        res = [[0] * n for _ in range(n)]
        #print(res)
        loop = n / 2
        x, y = 0, 0
        mid = int(n /2)
        count = 0
        offset = 1
        while loop >0:
            i = x
            j = y
            while j < y + n - offset:
                count += 1
                res[x][j] = count 
                j += 1
            while i < x + n - offset:
                count +=1
                res[i][j] = count
                i += 1
            while j > y:
                count += 1
                res[i][j] = count
                j -= 1
            while i > x:
                count += 1
                res[i][j] = count
                i -= 1
            
            x += 1
            y += 1
            offset += 2
            loop -= 1
        if n%2:
            count += 1
            res[mid][mid] = count
            print(res)
        return res

轮转数组/旋转链表/翻转字符串里的单词

给你一个数组，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。
示例：

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

class Solution(object):
    def rotate(self, nums, k):
        """
        :type nums: List[int]
        :type k: int
        :rtype: None Do not return anything, modify nums in-place instead.
        """
        #这个题的难点是怎么让代码做出论转的动作，一般的思路是当左右指针走到尽头了重新进行循环，试试看吧
        
        #定义一个轮转操作函数，变量是操作步长k，还有操作序列nums
        right = len(nums) - (k % len(nums)) #求步长的余数，如果刚好是数组的长度，则可以等于没走
        res = []
        #换个思路，再找一个数组，当right走了k步后，从零开始跟着right捡数据，right就负责反复遍历数组
        for i in range(len(nums)):
            #print(right)
            if right == len(nums):
                right = 0
            res.append(nums[right])
            right += 1
            print(res)
        for i in range(len(nums)):
            nums[i] = res[i]

翻转字符串单词问题(一次AC)

class Solution(object):
    def reverseWords(self, s):
        """
        :type s: str
        :rtype: str
        """
        #转换数列、遍历、切词、单个单词翻转函数、遍历完毕
        res = []
        s = list(s)
        left = 0
        right = 0
        def exchange(l,r,s):
            while l < r:
                    s[l], s[r-1] = s[r-1], s[l] 
                    l += 1
                    r -= 1
        while right != len(s):
            right += 1
            if  right == len(s) or s[right] == " ":
                #循环函数
                exchange(left,right,s)
                left = right + 1
        return "".join(s)

数组[列表]排序问题:手撕排序

leetcode排序
 解答

快速排序

class Solution(object):
    def sortArray(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        left = 0
        right = len(nums)-1
        nums = self.quicksort(left,right,nums)
        return nums
        #排序数组，手撕快排
    def quicksort(self,left,right,a):
        if left > right:
            return
        temp = a[left] #记下此时的基准数
        #更新左右哨兵标注i，j
        i = left
        j = right
        #print(j)
        while i != j:
            #哨兵移动,找逆差对，记得先右再左（很重要）
            while a[j] >= temp and i < j: #先从右往左找
                j -= 1
            while a[i] <= temp and i < j: #从左往右找
                i += 1
            if i < j: #如果没有碰头，交换数的位置
                t = a[j]
                a[j] = a[i]
                a[i] = t
        #i找到了中间，交换参考点
        a[left] = a[i] #重点放左边
        a[i] = temp #参考点给到中间
        #两边递归求解
        self.quicksort(left,i-1,a)
        self.quicksort(i+1,right,a) 
        return a

class Solution:
    def sortArray(self, nums: List[int]) -> List[int]:
        def partition(arr, low, high):
            pivot_idx = random.randint(low, high)                   # 随机选择pivot
            arr[low], arr[pivot_idx] = arr[pivot_idx], arr[low]     # pivot放置到最左边
            pivot = arr[low]                                        # 选取最左边为pivot
            left, right = low, high     # 双指针
            while left < right:
                while left<right and arr[right] >= pivot:          # 找到右边第一个<pivot的元素
                    right -= 1
                arr[left] = arr[right]                             # 并将其移动到left处           
                while left<right and arr[left] <= pivot:           # 找到左边第一个>pivot的元素
                    left += 1
                arr[right] = arr[left]                             # 并将其移动到right处
            arr[left] = pivot           # pivot放置到中间left=right处
            return left
        
        def quickSort(arr, low, high):
            if low >= high:             # 递归结束
                return  
            mid = partition(arr, low, high)     # 以mid为分割点，右边元素>左边元素
            quickSort(arr, low, mid-1)          # 递归对mid两侧元素进行排序
            quickSort(arr, mid+1, high)
        quickSort(nums, 0, len(nums)-1)         # 调用快排函数对nums进行排序
        return nums

堆排序
堆排序的思想就是先将待排序的序列建成大根堆，使得每个父节点的元素大于等于它的子节点。此时整个序列最大值即为堆顶元素，我们将其与末尾元素交换，使末尾元素为最大值，然后再调整堆顶元素使得剩下的 n-1 个元素仍为大根堆，再重复执行以上操作我们即能得到一个有序的序列。

class Solution:
    def max_heapify(self, heap, root, heap_len):
        p = root
        while p * 2 + 1 < heap_len:
            l, r = p * 2 + 1, p * 2 + 2
            if heap_len <= r or heap[r] < heap[l]:
                nex = l
            else:
                nex = r
            if heap[p] < heap[nex]:
                heap[p], heap[nex] = heap[nex], heap[p]
                p = nex
            else:
                break
        
    def build_heap(self, heap):
        for i in range(len(heap) - 1, -1, -1):
            self.max_heapify(heap, i, len(heap))

    def heap_sort(self, nums):
        self.build_heap(nums)
        for i in range(len(nums) - 1, -1, -1):
            nums[i], nums[0] = nums[0], nums[i]
            self.max_heapify(nums, 0, i)
            
    def sortArray(self, nums: List[int]) -> List[int]:
        self.heap_sort(nums)
        return nums

并归排序

class Solution:
    def merge_sort(self, nums, l, r):
        if l == r:
            return
        mid = (l + r) // 2
        self.merge_sort(nums, l, mid)
        self.merge_sort(nums, mid + 1, r)
        tmp = []
        i, j = l, mid + 1
        while i <= mid or j <= r:
            if i > mid or (j <= r and nums[j] < nums[i]):
                tmp.append(nums[j])
                j += 1
            else:
                tmp.append(nums[i])
                i += 1
        nums[l: r + 1] = tmp

    def sortArray(self, nums: List[int]) -> List[int]:
        self.merge_sort(nums, 0, len(nums) - 1)
        return nums

数组部分总结

数组是存放在 连续内存空间 上 相同类型数据 的集合

一些典型数组处理方法：
- 二分法：二分的难点在于升序/降序（下面以升序为例子）奇偶长度数组的边界处理，边界比较后如何选择新边界十分关键（是左1还是右1，大体逻辑就是，边界值大于目标值，则目标在左边，右边界移动到这，因为此处已经进行过计算，则可再向左移动一位，右边同理）
- 双指针法：针对双循环的题目，可以用一快一慢的指针减少时间复杂度(n^2→n)，比如对数组进行删除操作
- 滑动窗口法：滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。
- 螺旋矩阵——模拟行为法：
  相信大家又遇到过这种情况：感觉题目的边界调节超多，一波接着一波的判断，找边界，踩了东墙补西墙，好不容易运行通过了，代码写的十分冗余，毫无章法，其实真正解决题目的代码都是简洁的，或者有原则性的。

链表

什么是链表？

链表为一种通过指针串联在一起的线性结构，每一个节点有两部分组成，头和指针/数据域和指针域
最后一个节点的指针域指向null（其为空指针），相对应的，入口节点为头指针。
链表有单双链表和循环链表，在内存中独立散乱分布（和数组相区别）

移除节点

为了操作统一，可以虚拟一个头结点进行操作

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        // 删除头结点
        while (head != NULL && head->val == val) { // 注意这里不是if
            ListNode* tmp = head;
            head = head->next;
            delete tmp;
        }

        // 删除非头结点
        ListNode* cur = head;
        while (cur != NULL && cur->next!= NULL) {
            if (cur->next->val == val) {
                ListNode* tmp = cur->next;
                cur->next = cur->next->next;
                delete tmp;
            } else {
                cur = cur->next;
            }
        }
        return head;
    }
};

设计链表

设计链表就是编写一个具有功能函数的链表类，比如可以获取链表的某个值，插入删除某个节点，追加节点等等，示例

class Node:
    def __init__(self, val):
        self.val = val
        self.next = None
class MyLinkedList:

    def __init__(self):
        self._head = Node(0)
        self._count = 0

#获取第n个节点的值并返回
    def get(self, index: int) -> int:
        if 0 <= index < self._count:
            node = self._head
            for _ in rang(index + 1):
                node = node.next#node指针遍历到目标节点
            return node.val
        else:
            return -1

    def addAtHead(self, val: int) -> None:
        self.addAtIndex(0, val)

    def addAtTail(self, val: int) -> None:
        self.addAtIndex(self._count, val)

    def addAtIndex(self, index: int, val: int) -> None:
        if index < 0: #小于目标节点
            index = 0
        elif index > self._count:#目标节点大于列表，爆了
            return
        
        self._count +=1 #一个指针要先去到下一节点

        add_node = Node(val)
        prev_node, current_node = None, self._head #初始化
        for _ in range(index + 1):#移动
            prev_node, current_node = current_node, current_node.next
        else:#遇到
            prev_node.next, add_node.next = add_node, current_node#连接


    def deleteAtIndex(self, index: int) -> None:
        if 0 <= index < self._count:
            self._count -= 1
            prev_node, current_node = Node, self._head
            for _ in range(index + 1):
                prev_node, current_node = current_node, current_node.next
            else:
                prev_node, current_node = current_node.next, None

# 双链表
# 相对于单链表, Node新增了prev属性
class Node:
    
    def __init__(self, val):
        self.val = val
        self.prev = None
        self.next = None


class MyLinkedList:

    def __init__(self):
        self._head, self._tail = Node(0), Node(0)  # 虚拟节点
        self._head.next, self._tail.prev = self._tail, self._head
        self._count = 0  # 添加的节点数

    def _get_node(self, index: int) -> Node:
        # 当index小于_count//2时, 使用_head查找更快, 反之_tail更快
        if index >= self._count // 2:
            # 使用prev往前找
            node = self._tail
            for _ in range(self._count - index):
                node = node.prev
        else:
            # 使用next往后找
            node = self._head   
            for _ in range(index + 1):
                node = node.next
        return node

    def get(self, index: int) -> int:
        """
        Get the value of the index-th node in the linked list. If the index is invalid, return -1.
        """
        if 0 <= index < self._count:
            node = self._get_node(index)
            return node.val
        else:
            return -1

    def addAtHead(self, val: int) -> None:
        """
        Add a node of value val before the first element of the linked list. After the insertion, the new node will be the first node of the linked list.
        """
        self._update(self._head, self._head.next, val)

    def addAtTail(self, val: int) -> None:
        """
        Append a node of value val to the last element of the linked list.
        """
        self._update(self._tail.prev, self._tail, val)

    def addAtIndex(self, index: int, val: int) -> None:
        """
        Add a node of value val before the index-th node in the linked list. If index equals to the length of linked list, the node will be appended to the end of linked list. If index is greater than the length, the node will not be inserted.
        """
        if index < 0:
            index = 0
        elif index > self._count:
            return
        node = self._get_node(index)
        self._update(node.prev, node, val)

    def _update(self, prev: Node, next: Node, val: int) -> None:
        """
            更新节点
            :param prev: 相对于更新的前一个节点
            :param next: 相对于更新的后一个节点
            :param val:  要添加的节点值
        """
        # 计数累加
        self._count += 1
        node = Node(val)
        prev.next, next.prev = node, node
        node.prev, node.next = prev, next

    def deleteAtIndex(self, index: int) -> None:
        """
        Delete the index-th node in the linked list, if the index is valid.
        """
        if 0 <= index < self._count:
            node = self._get_node(index)
            # 计数-1
            self._count -= 1
            node.prev.next, node.next.prev = node.next, node.prev

# Your MyLinkedList object will be instantiated and called as such:
# obj = MyLinkedList()
# param_1 = obj.get(index)
# obj.addAtHead(val)
# obj.addAtTail(val)
# obj.addAtIndex(index,val)
# obj.deleteAtIndex(index)

翻转链表

要想进行链表的翻转，不是重新遍历（浪费内存空间），而是修改指针指向达到翻转的效果
例如双指针遍历，一次操作修改一次指针（为了统一程序的操作，采用虚拟头节点）
或者因为操作的内在一致性，可以想到使用递归的方法。

class Solution {
public:
    //双指针
    ListNode* reverseList(ListNode* head) {
        ListNode* temp;
        ListNode* cur = head;
        ListNode* pre = NULL;
        //cur为空时循环结束
        while(cur){
            temp = cur->next; //把当前下一节点的指向存起来
            cur->next = pre; //指针翻转到上一节点
            pre = cur; //向着翻转方向移动一位
            cur = temp; //同理，移动一位
        }
        return pre;

    }
};

递归法：

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        #递归
        if head == None or head.next == None:
            return head
        cur = self.reverseList(head.next) #一直递归到头，回溯返回head为最后的节点，给cur，此时head为倒数第二个节点
        head.next.next = head #用head.next表示最后的节点，再把next指向当前的倒数第二节点，完成翻转
        head.next = None #再把向后的指针青空
        return cur #向上一个递归循环返回当前cur（head） 但也是一直不变的head，用于最后输出

两两节点交换

依据代码的完整性逻辑，一般不改变节点值，而是进行实际的交换

删除链表的倒数N节点（三次AC）

双指针的经典应用，如果要删除【倒数】第n个节点：让fast移动n步，然后让fast和slow同时移动，直到fast指向链表末尾。删掉slow所指向的节点就可以了。（双指针对于位置距离的控制效果）

# Definition for singly-linked list.
# class ListNode(object):
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution(object):
    def removeNthFromEnd(self, head, n):
        """
        :type head: ListNode
        :type n: int
        :rtype: ListNode
        """
        # 要想删除链表中的某个节点，就要把前一个节点的next指向下一个节点，出了c其他语言不需要回收内存
        # 此处是删除倒数的链表节点，怎么样才能再不知道链表长度的情况下定位n呢，当然是用指针距离:要删除倒数第n个节点，pro距离cur必须为n
        # 为了更好的计数统计，使用虚拟的头节点
        nhead = ListNode(None,head)
        cur = nhead
        pro = head #前指针
        #cur.next = head #后指针
        count = 0
        #print(pro.next) #head原来就是第一个节点啊（写着写着恍然大悟）
        while pro.next != None: #前指针停在最后一个节点，此时要删节点了，跳出循环
            pro = pro.next #前指针前进
             #前指针移动了count次,
            count += 1
            if count >= n: #跟着走
                cur = cur.next    
        #当pro到终点
        cur.next = cur.next.next
        return nhead.next

链表相交

问题：给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。（题目中确保了链表没有环结构）
思路：这一题就是求两个链表交点处的指针。

环形链表II

哈希表（key:value/O1时间访问）

我理解的哈希表：
哈希表的本质：哈希(hash)映射算法，把传入的key值映射道符号表的索引上
哈希表的作用：快速查看元素是否出现在集合中（以时间换空间）
理解哈希函数的本质原理以及哈希碰撞在哈希表中的作用：多个key映射到相同索引上的情景，处理碰撞的普通方式是拉链法和线性探测法。

常见的三种哈希结构：数组，set，map
哈希表常考题型：给数据搜索数据中的某些元素或者寻求建立对应关系的题型，但凡涉及某个元素搜索的时空复杂度，都可以考虑哈希。

有效字母异位词

数组就是固定大小的简单哈希表，可以考虑采用相对数值计数的方法，给一个带下标的数组（哈希表）里不断计某个字母出现的次数，这样就可以判断这些字母是否共有，还能通过减操作判断其是否可以完美还原和复原其字母异位词。

#字母异位存在问题可以通过计数解决，也就是看两个字符串字母出现的次数是否相等，以下是伪代码
class Solution:
    def isAnagram(self, s, l):
        """
        :type s: str
        :type t: str
        :rtype: bool
        """
        #定义一个用来表示26个字母的数组（哈希表）
        recode = [0]*26
        #原字符串输入遍历记录 python中的ord是用来返回变量对应的ascall码
        for i in range(len(s)):
            recode[ord(s[i]) - ord('a')] += 1
        for j in range(len(l)):
            recode[ord(l[j]) - ord('a')] -= 1
        for k in range(26):
            if recode[k] != 0:
                return False  
        return True

两个数组的交集

题意：给定两个数组，编写一个函数来计算它们的交集。
这里要学一种结构：unordered_set 用于解决不考虑输出结果顺序的情况
值得注意的地方是数组是有限简单哈希表，这里没有著名数据的限制，所以无法使用数组而使用集合set(set预设占用空间比数组大，而且也比数组慢)

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> result_set; // 存放结果
        unordered_set<int> nums_set(nums1.begin(), nums1.end());
        for (int num : nums2) {
            // 发现nums2的元素 在nums_set里又出现过
            if (nums_set.find(num) != nums_set.end()) {
                result_set.insert(num);
            }
        }
        return vector<int>(result_set.begin(), result_set.end());
    }
};

快乐数

题意：编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」定义为：对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和，然后重复这个过程直到这个数变为 1，也可能是无限循环但始终变不到 1。如果可以变为 1，那么这个数就是快乐数。

```
#### 两数之和（下边刷题拓展4）
【基本】两数之和问题：给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target  的那 两个 整数，并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。你可以按任意顺序返回答案。
```python
#自己的思路
class Solution(object):
def twoSum(self, nums, target):
    """
    :type nums: List[int]
    :type target: int
    :rtype: List[int]
    """
    #内置函数enumerate()将数组等转化为可遍历序列
    #要解决两数和还要知道下标索引，自然是采用map和哈希
    record = dict()
    for idx, val in enumerate(nums):
        #值和下标一起遍历nums,找另一半是否在，不在就先存起来,记得存的是下标
        if target - val not in record:
            record[val] = idx
        else: 
            #如果在，说明之前存过了，都输出来即可
            return [record[target - val], idx]

一般暴力解法

class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
    n = len(nums)
    for i in range(n):
        for j in range(i + 1, n):
            if nums[i] + nums[j] == target:
                return [i, j]
    return []

三数之和

三数问题不同于两数问题，其中涉及去重是一个很复杂的工作，所以除非是返回数的下标索引这种不考虑动原数组的情况外，其他情况都考虑进行排序和双指针操作便于一开始就通过位置关系进行去重

class Solution(object):
    def threeSum(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        #做三数问题，首先思路清晰方法对
        #首先对nums进行排序
        nums.sort()
        res = []
        for i in range(len(nums)-1):
            #固定住了遍历位，等于后面找两个相加等于-nums[i]
            left = i + 1#避免重复
            right = len(nums)-1
            #解决一些首部出现连续相同数字的情况
            if nums[i] > 0: #排序后可知
                break
            if i >= 1 and nums[i] == nums[i-1]: #找最后那个不重复的i开始
                continue
            while left < right:
                #没找到三数，左也小于右那就一直找
                if nums[left] + nums[right] + nums[i] == 0:
                    res.append([nums[i],nums[left],nums[right]])
                    #此时也要判断是否只有这一个，局部去重
                    while left != right and nums[left] == nums[left+1]:
                        left += 1
                    while left != right and nums[right] == nums[right-1]:
                        right -= 1
                    left += 1
                    right -= 1
                elif nums[left] + nums[right] + nums[i] < 0:
                    left += 1
                else:
                    right -= 1
        return res

多位数的和与加

赎金信问题

题意：给定一个赎金信 (ransom) 字符串和一个杂志(magazine)字符串，判断第一个字符串 ransom 能不能由第二个字符串 magazines 里面的字符构成。如果可以构成，返回 true ；否则返回 false。
其实这道题和字母异位词问题很相似，都是求互相组成和成分查找的问题，自然而然首先想到使用哈希表。

字符串

反转字符串

将字符串转换成数组（自带“，”拆分），循环双头遍历互换实现字符串翻转，进阶问题就是添加一些判断条件和给题目加理解陷阱，如下翻转字符串||

def reverseStr(self, s, k):
        """
        :type s: str
        :type k: int
        :rtype: str
        """
        #长题目一定要梳理题意，本题就是要按2K长度切分字符串，然后把前半K翻转过来，剩下的不够也翻转，够了就翻转前半K
        res = list(s)
        # 设计局部翻转函数
        def reverse_str(text):
            left, right = 0, len(text) - 1
            while left < right:
                text[left], text[right] = text[right], text[left]
                left += 1
                right -= 1
            return text
        #遍历切分：这里是我还不会的局部切分步骤
        for cur in range(0, len(s), 2*k):
            print(cur)
            res[cur: cur + k] = reverse_str(res[cur: cur + k])
        return "".join(res)
        #先把问题模块化，这样最容易得到公共部分建立函数的思想以达到最简化程序的效果

替换空格

代码思路：

def replaceSpace(self, s: str) -> str:
        counter = s.count(' ')
        
        res = list(s)
        # 每碰到一个空格就多拓展两个格子，1 + 2 = 3个位置存’%20‘
        res.extend([' '] * counter * 2)
        
        # 原始字符串的末尾，拓展后的末尾
        left, right = len(s) - 1, len(res) - 1
        
        while left >= 0:
            if res[left] != ' ':
                res[right] = res[left]
                right -= 1
            else:
                # [right - 2, right), 左闭右开
                res[right - 2: right + 1] = '%20'
                right -= 3
            left -= 1
        return ''.join(res)

比较字符串的大小

给你两个版本号 version1 和 version2 ，请你比较它们

版本号由一个或多个修订号组成，各修订号由一个 ‘.’ 连接。每个修订号由多位数字组成，可能包含前导零。每个版本号至少包含一个字符。修订号从左到右编号，下标从 0 开始，最左边的修订号下标为 0 ，下一个修订号下标为 1 ，以此类推。例如，2.5.33 和 0.1 都是有效的版本号。

比较版本号时，请按从左到右的顺序依次比较它们的修订号。比较修订号时，只需比较忽略任何前导零后的整数值。也就是说，修订号 1 和修订号 001 相等。如果版本号没有指定某个下标处的修订号，则该修订号视为 0 。例如，版本 1.0 小于版本 1.1 ，因为它们下标为 0 的修订号相同，而下标为 1 的修订号分别为 0 和 1 ，0 < 1 。

返回规则如下：

如果 version1 > version2 返回 1，
如果 version1 < version2 返回 -1，
除此之外返回 0。

class Solution(object):
    def compareVersion(self, version1, version2):
        """
        :type version1: str
        :type version2: str
        :rtype: int
        """
        #先进行版号分割，再逐一对比
        v1 = version1.split(".")
        v2 = version2.split(".")
        i = 0
        while i <= max(len(v1)-1,len(v2)-1):
            if i <= len(v1)-1:
                d1 = 0
                for j in range(len(v1[i])):
                    d1 +=  (ord(v1[i][-j-1]) - ord('0')) * (10 ** j) #对比字符串的的ascall码
                print(d1)
            else:
                d1 = 0
            if i <= len(v2)-1:
                d2 = 0
                for j in range(len(v2[i])):
                    d2 +=  (ord(v2[i][-j-1]) - ord('0')) * (10 ** j)
                print(d2)
            else:
                d2 = 0
            if d1 > d2:
                return 1
            elif d2 > d1:
                return -1
            else:
                i += 1
        return 0

翻转字符串中的单词

左旋转字符

实现sreStr()

重复的子字符串

无重复最长子串（三次AC）

给定一个字符串 s ，请你找出其中不含有重复字符的最长子串的长度。

这个方法的好处就是只用遍历一次（O（n））而且不用针对每个元素找其最长子串，直接找，重复了就扔（至于为什么，因为两个相同的字母间隔决定了串长，要想更长，只能丢前找后）

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        #找子串肯定少不了遍历，最高要求就是一次遍历，要得到最长长度，想到滑动窗口，但应该还有不用遍历每个元素的方法
        s = list(s)
        # 简单直接去求这个子串(遍历的时候一直装不同的字母，直到重复字母出现，记下此时的长度，并把原来那一节丢掉，再往后继续装)
        res = []
        temp = 0
        for i in range(len(s)):
            #print(i)
            if s[i] in res:
                #print("判断"+str(s[i])+'在'+str(res))
                if len(res) > temp: #更新最大值
                    temp = len(res)
                    #print("局部最大子串"+str(res)+str(temp))
                #已经有重复了，要把之前的斩掉
                idx = res.index(s[i])
                #print("删去前："+str(res))
                for j in res[:idx+1]:
                    res.remove(j)
                    #print("删去后："+str(res))
            res.append(s[i]) #再把这个i放进去
        if len(res) <= temp:
            return temp
        else:
            return len(res)

滑动窗口法

1	`class Solution`

字符中的最长回文子串

数据结构：栈、堆、队列

栈：数据先进后出的存储方式
堆：堆是一种常见的树形结构，是一种特殊的完全二叉树，当且仅当满足所有节点的值总是不大于或不小于其父节点的值的完全二叉树被称之为堆。堆的这一种特性称之为堆序性（顾名思义，就是用树串（堆）起来的一坨东西）因此，在一个堆中，根节点是最大（或最小）节点。如果根节点最小，称之为小顶堆（或小根堆），如果根节点最大，称之为大顶堆（或大根堆）。堆的左右孩子没有大小的顺序。有最大堆或者最小堆的说法。
队列：数据先进先出的存储方式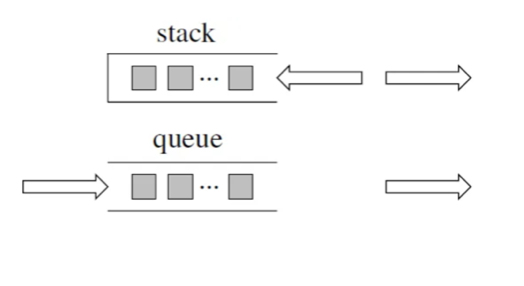

有效括号问题

给定一个只包括 ‘(‘，’)’，’{‘，’}’，’[‘，’]’ 的字符串，判断字符串是否有效。

有效字符串需满足：
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。

class Solution(object):
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """
        stack = []
        for item in s:
            if item == "(":
                stack.append(")")
            elif item == "[":
                stack.append("]")
            elif item == "{":
                stack.append("}")
            elif not stack or stack[-1] != item:
                return False
            else:
                stack.pop()
        #print(stack)
        if not stack:
            return True
        else:
            return False

碰碰消：删除字符串中所有的相邻重复游戏

class Solution(object):
    def removeDuplicates(self, s):
        """
        :type s: str
        :rtype: str
        """
        res = list()
        for item in s:
            if res and res[-1] == item:
                res.pop()
            else:
                res.append(item)
        return "".join(res)

二叉树/递归

二叉树是计算机底层的一种数据结构，有两大种类：满二叉树和完全二叉树

根据有无数据，又数据的又称为二叉搜索树，为有序树，有以下特点：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树
存储方式可以是数组，也可以是链表
二叉树的遍历（遍历问题学习递归，迭代的思想）

前序	中序	后序
中左右	左中右	左右中
从上到下	从左到右	从下倒上

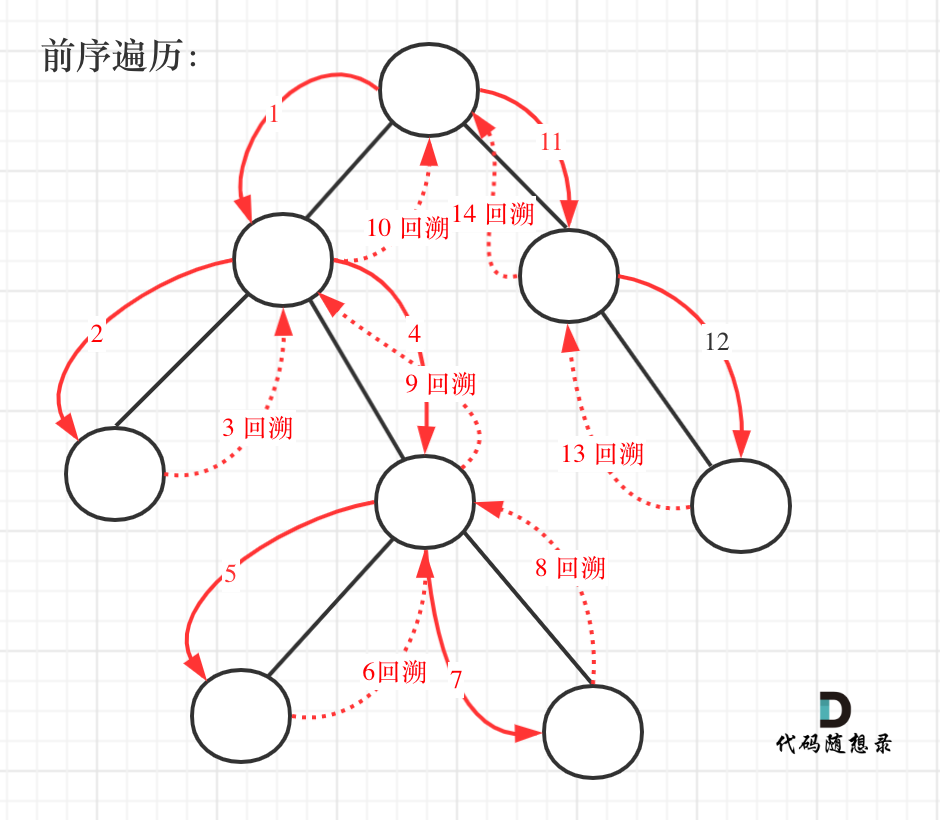
递归遍历：无限万花镜
递归的实现就是：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。

遇到过一种错误就是栈溢出，系统输出的异常是Segmentation fault（当然不是所有的Segmentation fault 都是栈溢出导致的），如果你使用了递归，就要想一想是不是无限递归了，那么系统调用栈就会溢出。

而且在企业项目开发中，尽量不要使用递归！在项目比较大的时候，由于参数多，全局变量等等，使用递归很容易判断不充分return的条件，非常容易无限递归（或者递归层级过深），造成栈溢出错误（这种问题还不好排查！）

我所理解的递归的根本思想就是函数“自我”的无限反复嵌套和不断进行穿参“求导”，直到最终求出最终的子节点（或者到达递归终点return回去的时候就变成了回溯），这就相当于把所有的节点按函数规定遍历的顺序遍历了一遍，拓展到同类问题也是一样的，当涉及到某一函数的大量重复调用的时候，也就是递归思想起作用的时候~

但迭代的本质依然是使用了栈的思想，每一次的递归调用都会把局部的变量，参数以及返回值压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。

经典代码如下：

//1.确定递归函数的具体参数和返回值
void digui(TreeNode* cur, vector<int>& vec)
//2.确定终止条件
    if (cur == NULL) return;
//3.确定单层递归的逻辑（带着不断递归来的参数在某一层应该怎么样操作，并且如何进行递归返回得到需要的结果）
    vec.push_back(cur->val);//收集当前值
    digui(cur->left, vec);//遍历左边
    digui(cur->right, vec);//遍历右边

迭代遍历：深度搜索
迭代顾名思义，用某种固定的方式函数对目标进行操作，和递归有相似之处（迭代更灵活一点）
前序遍历是中左右，每次先处理的是中间节点，那么先将根节点放入栈中，然后将右孩子加入栈，再加入左孩子。为什么要先加入右孩子，再加入左孩子呢？因为这样出栈的时候才是中左右的顺序。
迭代过程一定会用到栈操作，必须注意出入栈的顺序
经典代码：

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();                       // 中
            st.pop();
            result.push_back(node->val);
            if (node->right) st.push(node->right);           // 右（空节点不入栈）
            if (node->left) st.push(node->left);             // 左（空节点不入栈）
        }
        return result;
    }
};

层序遍历：广度搜索
就是从左到右一层一层的去遍历二叉树，需要借助一个辅助数据结构队列来实现，队列先进先出，符合一层一层遍历逻辑：

class Solution:
    """二叉树层序遍历迭代解法"""
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        results = []
        if not root:
            return results
        
        from collections import deque
        que = deque([root]) #把二叉树装进队列中
        
        while que:
            size = len(que)
            result = []
            #从头到尾，pop根append左右，最终直到que里没有节点
            for _ in range(size):
                cur = que.popleft() #当前节点从左边丢出去
                result.append(cur.val) #记录每个出来的点，就是层序节点值
                if cur.left:
                    que.append(cur.left) #子节点从右边捡回来
                if cur.right:
                    que.append(cur.right)
            results.append(result)

        return results

例题：填充每个节点的下一个右侧节点指针

class Solution(object):
    def connect(self, root):
        """
        :type root: Node
        :rtype: Node
        """
        #每一层的连接，广度搜索
        if not root:
            return root
        Q = collections.deque([root]) #第一层加入队列
        while Q:
            size = len(Q)
            for i in range(size): #遍历这一层所有的节点
                node = Q.popleft() #一般会pop左节点出来
                if i < size - 1:
                    node.next = Q[0] #等于右节点
                if node.left:
                    Q.append(node.left) #添加节点作为下一层计算
                if node.right:
                    Q.append(node.right)
        return root

锯齿遍历

if not root: #如果树的节点是空的，返回[]即可
            return []
        res = [] #初始化一个返回列表
        q = collections.deque() #初始化一个双边队列
        q.append(root) #首先将根节点压入双边队列中
        while q: #因为我们的目的就是将所有的节点遍历到，所以结束条件就是队列为空
            res_tmp = [] #因为题目要求返回的是按照层划分的数组，所以这边需要一个过渡数组
            n = len(q) #首先记录一下该层的长度，因为是每一层单边遍历记录，所以需要知道该层的长度
#因为队列还在不停的往里面压入这些节点的子孩子，所以q的长度是变化的，所以这边需要提前记录一下
            for i in range(n): #将每行所有的节点全部遍历到
                tmp = q.popleft() #首先将最左边的队列元素弹出
                res_tmp.append(tmp.val) #将弹出的节点值压入每行的过渡数组中
                if tmp.left: #如果当前节点存在左子树
                    q.append(tmp.left) #就把相应的左子树放入到队列中作为下一层待遍历的节点
                if tmp.right:#如果当前节点存在右子树
                    q.append(tmp.right)#就把相应的右子树放入到队列中作为下一层待遍历的节点
            res.append(res_tmp) #每层遍历结束，就将该层的遍历结果放入到最终的输出数组中
        for j in range(len(res)): #因为要求是锯齿遍历，所以要把偶数行给翻转一下
            if j % 2 == 1: #因为索引是从0开始的，所以这边判断余数是否为1
                res[j].reverse() #如果是第偶数行，翻转，reverse是一个自带的反转函数，蛮好用的
                
        return res #返回最终值即可

二叉树的属性

对称性：二叉树各内外侧（左右子节点）严格依据根节点为中轴轴对称
最大深度：根节点到树子节点的最长距离
最小深度：树子节点到根节点的最小距离
完全二叉树：左右子节点都存在的二叉树
平衡二叉树：左右两个子树的高度差的绝对值不超过1
二叉树的所有路径：
左叶子之和：注意判别左子叶的存在性，然后再进行遍历
找树左下角的值：本地要找出树的最后一行找到最左边的值。此时大家应该想起用层序遍历是非常简单的了，反而用递归的话会比较难一点。
树的路径总和：遍历的时候刻画路径
方法总结
二叉树：是否对称(opens new window)
递归：后序，比较的是根节点的左子树与右子树是不是相互翻转
迭代：使用队列/栈将两个节点顺序放入容器中进行比较
二叉树：求最大深度(opens new window)
递归：后序，求根节点最大高度就是最大深度，通过递归函数的返回值做计算树的高度
迭代：层序遍历
二叉树：求最小深度(opens new window)
递归：后序，求根节点最小高度就是最小深度，注意最小深度的定义
迭代：层序遍历
二叉树：求有多少个节点(opens new window)
递归：后序，通过递归函数的返回值计算节点数量
迭代：层序遍历
二叉树：是否平衡(opens new window)
递归：后序，注意后序求高度和前序求深度，递归过程判断高度差
迭代：效率很低，不推荐
二叉树：找所有路径(opens new window)
递归：前序，方便让父节点指向子节点，涉及回溯处理根节点到叶子的所有路径
迭代：一个栈模拟递归，一个栈来存放对应的遍历路径
二叉树：递归中如何隐藏着回溯(opens new window)
详解二叉树：找所有路径 (opens new window)中递归如何隐藏着回溯
二叉树：求左叶子之和(opens new window)
递归：后序，必须三层约束条件，才能判断是否是左叶子。
迭代：直接模拟后序遍历
二叉树：求左下角的值(opens new window)
递归：顺序无所谓，优先左孩子搜索，同时找深度最大的叶子节点。
迭代：层序遍历找最后一行最左边
二叉树：求路径总和(opens new window)
递归：顺序无所谓，递归函数返回值为bool类型是为了搜索一条边，没有返回值是搜索整棵树。
迭代：栈里元素不仅要记录节点指针，还要记录从头结点到该节点的路径数值总和
二叉树的修改与构造

翻转二叉树
构造二叉树（从中序遍历或者是后序遍历）
最大二叉树
合并二叉树
给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

思路：遍历操作，同事传入两个树的节点，同时操作。

解题思路

二叉搜索树中的插入操作(opens new window)
递归：顺序无所谓，通过递归函数返回值添加节点
迭代：按序遍历，需要记录插入父节点，这样才能做插入操作
二叉搜索树中的删除操作(opens new window)
递归：前序，想清楚删除非叶子节点的情况
迭代：有序遍历，较复杂
修剪二叉搜索树(opens new window)
递归：前序，通过递归函数返回值删除节点
迭代：有序遍历，较复杂
构造二叉搜索树(opens new window)
递归：前序，数组中间节点分割
迭代：较复杂，通过三个队列来模拟

求二叉搜索树的属性

二叉搜索树是一个有序树：
- 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
- 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
- 它的左、右子树也分别为二叉搜索树

这就决定了，二叉搜索树，递归遍历和迭代遍历和普通二叉树都不一样。

红黑树又叫平衡二叉搜索树，但它是在计算机科学中用来组织数据比如数字的块的一种结构。红黑树是一种平衡二叉查找树的变体，它的左右子树高差有可能大于1，所以红黑树不是严格意义上的平衡二叉搜索树。

二叉搜索树中的搜索
搜索二叉树节点中的某个值，并返回以该节点为根的子树。如果节点不存在，则返回NULL
验证二叉搜索树
知道中序遍历下，输出的二叉搜索树节点的数值是有序序列。
有了这个特性，验证二叉搜索树，就相当于变成了判断一个序列是不是递增的了。
二叉搜索树中的绝对误差
二叉搜索树中的众数
把二叉搜索树转换为累加树

公共祖先问题

二叉树的最近公共祖先
递归：后序，回溯，找到左子树出现目标值，右子树节点目标值的节点。
迭代：不适合模拟回溯

class Solution:
    """二叉树的最近公共祖先 递归法"""
    #递归思考，有返回值（祖先），参数（逐层遍历的root），单层：搜索，找到后返回
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if not root or root == p or root == q: #寻找目标节点
            return root
        
        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)
        
        if left and right: #两边都有返回值，说明找到了祖先当前root
            return root
        if left:
            return left
        return right

二叉搜索树的最近公共祖先
递归：顺序无所谓，如果节点的数值在目标区间就是最近公共祖先
迭代：按序遍历

class Solution(object):
    def lowestCommonAncestor(self, root, p, q):
        """
        :type root: TreeNode
        :type p: TreeNode
        :type q: TreeNode
        :rtype: TreeNode
        """
        #依然采用递归的遍历迭代方法，但只要求找到root的值在p,q之间
        if root.val > p.val and root.val > q.val:
            left = self.lowestCommonAncestor(root.left,p,q)#root大过右边了
            return left
        if root.val < p.val and root.val < q.val: #root小过左边了
            right = self.lowestCommonAncestor(root.right,p,q)
            return right
        return root #只为了找一个点然后递归返回

二叉树的修改与构造

二叉搜索树中的插入操作
删除二叉搜索树中的节点
修剪二叉搜索树
将有序数组转换为二叉搜索树
解题思路总结
二叉搜索树中的插入操作(opens new window)
递归：顺序无所谓，通过递归函数返回值添加节点
迭代：按序遍历，需要记录插入父节点，这样才能做插入操作
二叉搜索树中的删除操作(opens new window)
递归：前序，想清楚删除非叶子节点的情况
迭代：有序遍历，较复杂
修剪二叉搜索树(opens new window)
递归：前序，通过递归函数返回值删除节点
迭代：有序遍历，较复杂
构造二叉搜索树(opens new window)
递归：前序，数组中间节点分割
迭代：较复杂，通过三个队列来模拟

常见算法

贪心算法

什么是贪心

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。

这么说有点抽象，来举一个例子：

例如，有一堆钞票，你可以拿走十张，如果想达到最大的金额，你要怎么拿？指定每次拿最大的，最终结果就是拿走最大数额的钱。每次拿最大的就是局部最优，最后拿走最大数额的钱就是推出全局最优。
再举一个例子如果是有一堆盒子，你有一个背包体积为n，如何把背包尽可能装满，如果还每次选最大的盒子，就不行了。这时候就需要动态规划。动态规划的问题在下一个系列会详细讲解。

分发饼干问题

tips：当你想到要用双循环暴力解决问题的时候，看看能否可以只用一个循环就能完成两个量的转换

leetcode题目描述：
假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

我的题解代码：（暴力双循环遍历：一般来说容易超时）

def findContentChildren(self, g, s):
        
        # :type g: List[int]
        # :type s: List[int]
        # :rtype: int
        
        #先给两个数组进行重排
        gg = sorted(g)
        #print(gg)
        ss = sorted(s)
        #print(ss)
        # 双重遍历知否满足
        count = 0
        for i in gg: #给每个孩子发饼干
            print(ss)
            for j in ss:
                if j >= i:
                    #饼干每吃一块就少一块,python有三种删除节点的方法，list.remove():删除某个元素 del list[i]：删除某个下标元素 list.pop(i):栈的抛出
                    ss.remove(j)
                    count += 1
                    break
                else:
                    continue
        return count

随想录题解：思路是这样的，贪心的地方是大饼干就先满足胃口大的孩子，所以顺序数组里遍历大胃口的孩纸后吃掉的同时索引也能递减1，用下一块大饼满足下一大胃王，直到最后遍历结束

def findContentChildren(self, g, s):
        
        # :type g: List[int]
        # :type s: List[int]
        # :rtype: int
        
        gg = sorted(g)
        ss = sorted(s)
        count = 0
        index = len(ss) - 1
        i = len(gg) - 1
        #print(index)
        #排序可以值得知道有序遍历的结果
        while index >= 0 and i >= 0:
            if  ss[index] >= gg[i]:
                count += 1
                index -= 1 #索引跟着目录递减
            i -= 1
        return count

摆动序列问题：独立做出来的第一道中等题

思路：我想到的和题解差不多，主要思路都是删除或者找到局部峰值从而得到全局最优，难点在于如何处理两边端点处的峰值。我采用的是分类举例逐渐删除连续点，随想录的方法简洁很多，统计峰值，其实和我一开始设计的循环判定类似，但是我没有处理好遍历方式，导致刚开始代码没有AC

class Solution(object):
    def wiggleMaxLength(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        #log = len(nums) - 1 #下标
        print(log)
        i = 0
        # if len(nums) == 1:
        #     return 1
        # if len(nums) <3 and len(nums) > 1:
        #     if nums[0] == nums[1]:
        #         return 1
        #     elif nums[0] != nums[1]:
        #         return 2
        # if len(nums) >=3:
        if len(nums) == 1:
                return 1
        if len(nums) == 2:
            if nums[0] == nums[1]:
                return 1
            elif nums[0] != nums[1]:
                return 2
        while i <= len(nums) - 3 :
            #遍
            if len(nums) == 1:
                return 1
            if len(nums) == 2:
                if nums[0] == nums[1]:
                    return 1
                elif nums[0] != nums[1]:
                    return 2
            print(nums)
            print(i)
            if nums[i] <= nums[i+1] and nums[i+1] <= nums[i+2]:
                del nums[i+1]
                print("删除后"+str(nums))
                if len(nums) == 1:
                    return 1
                if len(nums) == 2:
                    if nums[0] == nums[1]:
                        return 1
                    elif nums[0] != nums[1]:
                        return 2
            elif nums[i] >= nums[i+1] and nums[i+1] >= nums[i+2]:
                del nums[i+1]
                print("删除后"+str(nums))
                if len(nums) == 1:
                    return 1
                if len(nums) == 2:
                    if nums[0] == nums[1]:
                        return 1
                    elif nums[0] != nums[1]:
                        return 2
            else:
                i += 1
        #print(nums)
        return len(nums)

class Solution(object):
    def wiggleMaxLength(self, nums):
        if len(nums) <= 1: return len(nums)
        i = 0
        res = 1 #默认左边有一个
        predif = 0
        while i < len(nums) - 1: #初始化变量一般都要放在循环外，不然每次循环都会初始化一次
            curdif = nums[i + 1] - nums[i]
            i += 1
            if (curdif >0 and predif <= 0) or (predif >=0 and curdif < 0):
                res += 1
                predif = curdif
        return res

最大子序列和

其实是个DP问题，但可以发现局部贪心无返利，由此可以推出全局最优解

def maxSubArray(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        #直接逐个遍历的暴力解法也很方便，但局部还可以继续优化，所以可以用贪心算法，根据题意，当我的子数组合出现负值时，说明前面的子序已经不能用了，加了只会拖累总和，所以从下一个开始继续重新计数
        count = 0 #计数器
        i = 0 #数组遍历标志位
        max = -10^4
        while i <= len(nums) - 1:
            pro = count
            count += nums[i]
            if count > max:
                max = count
            if count < 0:
                count = 0
                pro = 0
            i += 1
        return max

经典问题:股票买卖获得的最大收益

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择某一天买入这只股票，并选择在未来的某一个不同的日子卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。
贪心：

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        cur = 99999999999999999
                maxgot = 0
                for curprice in prices:
                    got = 0
                    if curprice < cur:
                        cur = curprice
                    else:
                        got = curprice - cur
                    if got > maxgot:
                        maxgot = got
                    else:
                        pass
                return maxgot

动态规划：

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n = len(prices)
        if n == 0: return 0 # 边界条件
        dp = [0] * n
        minprice = prices[0] 

        for i in range(1, n):
            minprice = min(minprice, prices[i])
            dp[i] = max(dp[i - 1], prices[i] - minprice)

        return dp[-1]

回溯算法

回溯其实是不断进行递归搜索的for循环，就好像你想把10个数进行两两的组合，就要用双层for循环遍历
那100个数进行十十组合了，全部写出来不现实，所以要采用回溯算法在每传入一个递归参数（+1）时可以顺利地完成所有的组合

组合问题

高维组合问题是经典的回溯算法应用问题

分割回文串问题

子集问题

动态规划

什么是DP（动态规划）

动态规划中每一个状态一定是由上一个状态推导出来的，这一点区分于贪心算法，贪心没有状态推倒关系，而是模拟局部最优解获得全局最优解（孤儿求强）。例如背包问题，动态规划dp[j]是由dp[j-weight]推倒就最直而来，贪心则是每次都拿最大的就可以了
应用场合: 动态规划又称之为DP，如果某一问题有很多重叠子问题，使用动态规划的方法是最有效的

解题步骤（动规五部曲）

关注问题：DP数组下标的含义，递推公式，DP数组如何初始化，遍历顺序

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组

DP如何debug

找问题的最好方式就是把dp数组打印出来，看看究竟是不是按照自己思路推导的！
做动规的题目，写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍，心中有数，确定最后推出的是想要的结果。然后再写代码，如果代码没通过就打印dp数组，看看是不是和自己预先推导的哪里不一样。
如果打印出来和自己预先模拟推导是一样的，那么就是自己的递归公式、初始化或者遍历顺序有问题了。如果和自己预先模拟推导的不一样，那么就是代码实现细节有问题。
这样才是一个完整的思考过程，而不是一旦代码出问题，就毫无头绪的东改改西改改，最后过不了，或者说是稀里糊涂的过了。

背包问题

打家劫舍

股票问题

子序列问题

找最长子序列

深度优先搜索算法DFS

深度优先搜索：
深度优先搜索是搜索的一种方式，根本是使用堆栈和递归操作，将多节点的某分支/沿某一方向搜索到底的算法。
图像渲染问题

class Solution(object):
    def floodFill(self, image, sr, sc, newColor):
        """
        :type image: List[List[int]]
        :type sr: int
        :type sc: int
        :type newColor: int
        :rtype: List[List[int]]
        """
        R, C = len(image), len(image[0])#获取图像的长和宽
        color = image[sr][sc] #初始值颜色
        if color == newColor: return image
        def dfs(r, c):
            if image[r][c] == color: #如果和初始值一样，渲染
                image[r][c] = newColor
                if r >= 1:  #然后看上下左右是否合适进行递归搜索
                    dfs(r-1, c)
                if r+1 < R:
                    dfs(r+1, c)
                if c >= 1:
                    dfs(r, c-1)
                if c+1 < C:
                    dfs(r,c+1)
        dfs(sr, sc) #引用递归
        return image

广度优先搜索算法BFS

广度优先搜索适合搜索离初始点较近距离的目标值，因为它是多路共同发力，层层递进地去寻找目标值
图像渲染问题

class Solution:
    def floodFill(self, image: List[List[int]], sr: int, sc: int, newColor: int) -> List[List[int]]:
        currColor = image[sr][sc]
        if currColor == newColor:
            return image
        
        n, m = len(image), len(image[0])
        que = collections.deque([(sr, sc)])
        image[sr][sc] = newColor
        while que:
            x, y = que.popleft()
            for mx, my in [(x - 1, y), (x + 1, y), (x, y - 1), (x, y + 1)]:
                if 0 <= mx < n and 0 <= my < m and image[mx][my] == currColor:
                    que.append((mx, my))
                    image[mx][my] = newColor
        
        return image

刷题总结，代码随想录就是一个刷题套路集合

跟着代码随想录刷题，不知不觉这篇日志就成了万字长文，几个月的刷题，收获不多不少，但对提升代码的理解和解决问题的思维很有帮助~感谢Carl师兄！（为此特意在京东补购了一本方便以后随时翻阅）
这次可以说是从零基础开始的刷题，从数据结构到算法应用，复习了曾经学过的数组、链表以及字符串，新了解哈希表、二叉树这两种数据结构，新学习了贪心，回溯，动规等很有意义的解题思路和方法，当然，在解决各个问题的过程中还有很多的精华思路（比如双指针操作链表，操作链表的元素，推导判断链表是否有环，对数组进行二分查找，操作数组，使用哈希表进行快速查询，以及二叉树的遍历中学会的递归和迭代）

套路总结

套路	方法
递归三部曲	1.返回值参数 2.递归终止条件 3.单层逻辑
回溯三部曲	1.返回值参数 2.递归终止条件 3.单层逻辑
动规五部曲	1.确定dp数组以及含义 2.确定递推公式 3.dp数组如何初始化 4.确定遍历顺序 5.举例推导一下

后面，我会开始边投递简历边开始在牛客网熟悉ACM模式解题，顺便复习曾经学过的套路

以后的纯刷题部分

ACM模式python输入输出方法OJ

#单个输入
n = input()
#map接收单行多个
nums = list(map(int,input().split()))
#分收两个
x, y = map(int,input().split().split())
#接收多行
while True:
    try:
        nums = list(map(int,input().split()))
    except:
        break
# 循环输入
n, x = [int(s) for s in input().split()]
# 序列输入
score = [int(s) for s in input().split()]

拿到这道题直接就想到了双循环遍历然后计数，是很显然的方法，但问题就是复杂度太高了，吃满数组内存运行起来又是N的平方，数据量一大就是指数型爆炸的运算量，其实最好的方法有排序法和哈希表法！

排序测邻：优势，排序的复杂度只有logN，要比双循环好，而且有sorted（）、set（）这种直接处理序列的API，实现起来很方便。

class Solution {
public:
    bool containsDuplicate(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int n = nums.size();
        for (int i = 0; i < n - 1; i++) {
            if (nums[i] == nums[i + 1]) {
                return true;
            }
        }
        return false;
    }
};

哈希表：对于数组中每个元素，我们将它插入到哈希表中。如果插入一个元素时发现该元素已经存在于哈希表中，则说明存在重复的元素。

class Solution {
public:
    bool containsDuplicate(vector<int>& nums) {
        unordered_set<int> s;
        for (int x: nums) {
            if (s.find(x) != s.end()) {
                return true;
            }
            s.insert(x);
        }
        return false;
    }
};

递归思想解决斐波那数列问题

为什么想到递归方法，因为递推过程每一层的操作是一样的，解决的问题具备重复的单层逻辑就可以采用递归策略，然后再设计出相应的返回值、变量和终止条件

class Solution(object):
def fib(self, n):
    """
    :type n: int
    :rtype: int
    """
    dp = [0,1]
    i = 2
    self.diguifa(dp,i,n) #类内的自调用和相互调用一般都需要self作为实例参数
    #print(dp)
    return dp[n]

def diguifa(self,dp,i,n):
    if i <= n:
        temp = dp[i-1] +dp[i-2]
        #print(temp)
        dp.append(temp)
        self.diguifa(dp,i+1,n)
    else:
        return

移动零问题

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。
请注意必须在不复制数组的情况下原地对数组进行操作。

class Solution(object):
def moveZeroes(self, nums):
    """
    :type nums: List[int]
    :rtype: None Do not return anything, modify nums in-place instead.
    """
    #应该是很经典的双指针，前一个指针遍历，后一个指针用来把0往后推（原始做法）,
    #还可以用删除计数，最后再nums末尾补0的方法，但会改变数组的尺寸，导致不好遍历，得想点办法:换个遍历方式不就行了！for range是枚举式遍历，不好控制进度，那就使用带条件的循环遍历
    #left, right = 0, len(nums)-1
    count = 0
    i = 0
    while i <= len(nums)-1:
        print(i)
        if nums[i] == 0:
            nums.pop(i)
            count += 1
        else:
            i += 1
    print(nums)
    for i in range(count):
        nums.append(0)
    return nums

两数之和/n数之和问题拓展：

输入有序数组问题：给你一个下标从 1 开始的整数数组 numbers ，该数组已按非递减顺序排列，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。你所设计的解决方案必须只使用常量级的额外空间。

class Solution(object):
def twoSum(self, numbers, target):
    """
    :type numbers: List[int]
    :type target: int
    :rtype: List[int]
    """
    #二分法的要求是数组有序且无重复，题意好像不满足无重复
    #与其两次循环遍历，不如一次遍历，一次二分查找降低复杂度
    #循环到一个数，拿target减去他，在后面的数里进行二分查找（因为如果是前面的，那肯定已经找出来了），最后组合数组
    for i in range(len(numbers)):
        tar2 = target - numbers[i]
        left, right = i, len(numbers)-1
        while left <= right:
            mid = (left + right) / 2
            #print(mid)
            if numbers[mid] < tar2:
                #目标在右，左指针动
                left = mid + 1
            elif numbers[mid] == tar2:
                #找到了，返回
                if mid == i: #判定同时出现两个相同的数后使用到了同一个下标,如果一开始就让left+1的话可以避免这个问题（官方解答）
                    mid = i + 1
                    return [i+1,mid+1]
                else:
                    return [i+1,mid+1] #示例比下标索引多1
            else:
                #目标在左
                right = mid - 1       
    return [-1,-1]

链表中间节点问题(一次AC)

给定一个头结点为 head 的非空单链表，返回链表的中间结点。如果有两个中间结点，则返回第二个中间结点。

class Solution(object):
    def middleNode(self, head):
        """
        :type head: ListNode
        :rtype: ListNode
        """
        # 直接写？不对，应该用一个指针与另外一个指针始终保持两倍的距离关系
        cur = head
        count = 0
        def togo(step):
            pro = head
            while step != 0:
                pro = pro.next
                step -= 1
            return pro
        while cur != None:
            cur = cur.next
            count += 1 
        #count % 2 == 0:
        #是偶数，输出右边节点
        step = int(count / 2)
        pro = togo(step)
        return pro
        # else:
        #     step = count / 2
        #     pro = togo(step)
        #     return pro

旋转序列求最大子序问题(DP法)

小美请小团吃回转寿司。转盘上有N盘寿司围成一圈，第1盘与第2盘相邻，第2盘与第3盘相邻，…，第N-1盘与第N盘相邻，第N盘与第1盘相邻。小团认为第i盘寿司的美味值为A[i]（可能是负值，如果小团讨厌这盘寿司）。现在，小团要在转盘上选出连续的若干盘寿司，使得这些寿司的美味值之和最大（允许不选任何寿司，此时美味值总和为0）。
输入：第一行输入一个整数T（1<=T<=10），表示数据组数。每组数据占两行，第一行输入一个整数N（1<=N<=10^5）；第二行输入N个由空格隔开的整数，表示A[1]到A[N]（-10^4<=A[i]<=10^4）。

输出：每组数据输出占一行，输出一个整数，表示连续若干盘寿司的美味值之和的最大值。

def findMaxSum(N,score):
'''
动态规划的想法：
pre[i]储存以第i个数结尾的连续数组的最大和，这样的连续数组只有两种可能
第一种，这个数组只有一个数，即第i个数
第二种，这个数组多于一个数，那么就是第i个数加以第i-1个数结尾的连续数组的最大和pre[i-1]
取这两个值的最大值
'''
pre = [0] #为什么提前设0，这里是初始化pre[i]，让pre在i+1的地方append以i为结尾的最大值
for i in range(N):
    maxSum = max(score[i],score[i]+pre[i])
    pre.append(maxSum) 
return max(pre)
 
 
T = int(input())
while T:
    T = T-1
    N = int(input())
    score = list(map(int, input().split()))
    maximum = findMaxSum(N,score)
    minimum = findMaxSum(N,[-i for i in score])
    if sum(score)+minimum>maximum:
        maximum = sum(score)+minimum
    print(maximum)

无向图和有向图

小团找到一颗有n个节点的苹果树，以1号节点为根，且每个节点都有一个苹果，苹果都有一个颜色，但是这棵树被施加了咒术，这使得小团只能从某一个节点的子树中选取某一种颜色的拿。小团想要拿到数量最多的那种颜色的所有苹果，请帮帮她。每次她会指定一个节点t，如果小团只能从节点t的子树中选取某一种颜色的苹果，选取什么颜色能拿到最多的苹果？如果有多种颜色都可以拿同样多的苹果，输出颜色编号最小的那个对应的编号。节点x的子树定义为所有将x当作祖先的节点，x也视为x的子树的一部分。

题目中只告诉我们1为根节点，因此在输入两个有边相连的节点时，我们并不知道哪个是父节点哪个是子节点，需要先构建无向图的邻接表。然后从根节点1开始，自顶向下删去子节点指向父节点的关系，将无向图修改为有向图。
在每次query的过程中，利用bfs求得每个节点 t 的子树对应的所有节点，然后对节点颜色进行计数，输出出现最多且编号最小的颜色即可。

from queue import Queue
from collections import defaultdict

def bfs(root, tree):
    queue = Queue()
    queue.put(root)
    children = [root]
    while not queue.empty():
        cur = queue.get()
        if cur in tree:
            # 还没到叶子节点
            for child in tree[cur]:
                queue.put(child)
                children.append(child)
    return children

def modify(root):
    if tree[root]:
        for child in tree[root]:
            # 将子节点指向父节点的关系删除
            tree[child].remove(root)
            modify(child)

if __name__ == "__main__":
    n = int(input())
    tree = defaultdict(lambda: [])
    for _ in range(n - 1):
        x, y = map(int, input().strip().split())
        tree[x].append(y)
        tree[y].append(x)
    # 根据拓扑关系，将树改为有向图
    modify(1)
    colors = tuple(map(int, input().strip().split()))
    q = int(input())
    for _ in range(q):
        t = int(input())
        # bfs获得节点t的所有子节点(包括自己)
        children = bfs(t, tree)
        # 颜色计数器
        counter = defaultdict(lambda: 0)
        for child in children:
            counter[colors[child - 1]] += 1
        # 输出数量最多的颜色
        maxColor = 5001
        maxCount = 0
        for color in counter:
            if maxCount < counter[color]:
                maxCount = counter[color]
                maxColor = color
            elif maxCount == counter[color]:
                maxColor = min(color, maxColor)
        print(maxColor)

神秘代码问题

对于一个长度为n的字符串s，其对应的加密字符串t的第一个字符是s中的第n/2个字符（向上取整），而t中的第二个到第n个字符则刚好对应s删去第n/2个字符（向上取整）后所得字符串的加密字符串。这个规则也可以用如下流程描述：将t初始化为一个空串，不断从s中取出第n / 2个字符（向上取整），并将其拼到t的后面，当s为空时，t即是所求的加密字符串。设计命令行工具加密解密。

import math
class Solution():
    def secret(self, string, num, t): #选择加密解密模式
        if t == 1:
            return self.type1(string, num)
        if t == 2:
            return self.type2(string, num)
    #取字符方法，也有直接暴力删除的方式
    def type1(self, strings, nums):  #加密
        strings = '0' + strings #补首0移位,让下标数字自然对应字符串位数
        res = []
        temp = 0
        mininum = 1000000000
        while temp < nums:
            a = math.ceil((nums - temp)/2) #求第n/2个字符（向上取整）位置，但是要取的要么在左，要么在右，所以要加入如下判断
            if a < mininum:
                res.append(strings[a]) #拼接到a后
            else:
                res.append(strings[a+temp])#当a等于min，代表要append字符串后半段了
            mininum = min(a, mininum)# 取最小字符位置
            temp += 1
        return res

    def type2(self, strings, nums):
        strings = '0' + strings
        res = [0 for i in range(nums+1)]
        temp = 0
        index = 1
        mininum = 1000000000
        while temp < nums:
            a = math.ceil((nums - temp)/2)
            if a < mininum:
                res[a] = strings[index]
            else:
                res[a + temp] = strings[index]
            mininum = min(a, mininum)
            temp += 1
            index += 1
        del res[0] #去0
        return res

#输入输出样例
a = Solution()
string = 'hhhaaa'
num = 6
t = 2
r = a.secret(string, num, t)
print(" ".join(r))
#输出“ahhhaa”

分鸡蛋的教训：鸡蛋一般都不会只在一个篮子里

京东笔试分鸡蛋问题，一个大妈手里有x的鸡蛋，每次要么去鸡窝里拿一个，要么在手里能分三份的情况下分两份给别人，问什么时候可以手里拥有y个鸡蛋

T = 1
while T > 0:
    T -= 1
    x, y = 25, 9
    #print(x,y)
    count = 0
    temp = 0
    while x != y:
            near = 3 * (int(x / 3) + 1) #找最近的
            #print(near)
            std = list(range(x,temp))
            print(std)
            if y in std:
                count += y-x
                x = y
            elif x % 3 == 0:
                temp = x
                x = int(x / 3)
                count += 1
            else:
                count += near - x
                x = near
            print(x)
print(int(count))

LRU缓存机制
leetcode

#哈希表+双向链表
class ListNode:
    def __init__(self, key=None, value=None):
        self.key = key
        self.value = value
        self.prev = None
        self.next = None


class LRUCache:
    def __init__(self, capacity: int):
        self.capacity = capacity
        self.hashmap = {}
        # 新建两个节点 head 和 tail
        self.head = ListNode()
        self.tail = ListNode()
        # 初始化链表为 head <-> tail
        self.head.next = self.tail
        self.tail.prev = self.head

    # 因为get与put操作都可能需要将双向链表中的某个节点移到头部(变成最新访问的)，所以定义一个移动方法
    def move_node_to_header(self, key):
            # 先将哈希表key指向的节点拎出来，为了简洁起名node
            #      hashmap[key]                               hashmap[key]
            #           |                                          |
            #           V              -->                         V
            # prev <-> node <-> next         pre <-> next   ...   node
            node = self.hashmap[key]
            node.prev.next = node.next
            node.next.prev = node.prev
            # 之后将node插入到头部节点前
            #                   hashmap[key]                     hashmap[key]
            #                       |                                 |
            #                       V        -->                      V
            # header <-> next  ... node                   header <-> node <-> next
            node.prev = self.head
            node.next = self.head.next
            self.head.next.prev = node
            self.head.next = node
            
    def add_node_to_header(self, key,value):
        new = ListNode(key, value)
        self.hashmap[key] = new
        new.prev = self.head
        new.next = self.head.next
        self.head.next.prev = new
        self.head.next = new
        
    def pop_tail(self):
        last_node = self.tail.prev
        # 去掉链表尾部的节点在哈希表的对应项
        self.hashmap.pop(last_node.key)
        # 去掉最久没有被访问过的节点，即尾部Tail之前的一个节点
        last_node.prev.next = self.tail
        self.tail.prev = last_node.prev
        return last_node
    
    def get(self, key: int) -> int:
        if key in self.hashmap:
            # 如果已经在链表中了久把它移到头部（变成最新访问的）
            self.move_node_to_header(key)
        res = self.hashmap.get(key, -1)
        if res == -1:
            return res
        else:
            return res.value

    def put(self, key: int, value: int) -> None:
        if key in self.hashmap:
            # 如果key本身已经在哈希表中了就不需要在链表中加入新的节点
            # 但是需要更新字典该值对应节点的value
            self.hashmap[key].value = value
            # 之后将该节点移到链表头部
            self.move_node_to_header(key)
        else:
            if len(self.hashmap) >= self.capacity:
            # 若cache容量已满，删除cache中最不常用的节点 
                self.pop_tail()
            self.add_node_to_header(key,value)

摸鱼问题：
一个打工仔，一开始工作效率是1，每分钟后增加1，最高是M，M后还能干T分钟，不然得歇息10分钟重新从1开始发力，或者他中途任意时刻都能选择摸鱼5分钟，之后再从摸鱼前一半的搬砖速度开始干起，直到干完任务量N。

#摸鱼问题
N,M,T = [int(s) for s in input().split()]
#找时间最优问题，一种是干到M后强制休息10分钟重新从1开始，一种是中途任何时候选择摸鱼5分钟，效率仅为之前的一半
speed = 1 #初始工作效率
#贪心，因为摸鱼等于5分钟后从一半启动，肝满T等于从1启动，所以肝到T-1，然后摸鱼，以此循环
t = 0
Tt = T
while N > 0:
    if speed == M:
        Tt -= 1
        N -= speed
        if Tt == 1 and (N-speed)>0:
            #下一步已经做不完了，可以开始摸鱼，一开始N<speed可以一步做完这个情况想漏了，告诉我每次if else前是否把启动一个事件的必要条件考虑周全，不然就是某些莫名的bug
            t += 5
            speed = int(speed / 2)
            Tt = T
    else:
        N -= speed
        speed += 1
    t += 1
print(t)

面试题：创建一个可以找最小的堆class，并在0(1)时间内返回

class MinStack(object):
    def __init__(self):
        self.stack = []  # 存放所有元素
        self.minStack = []  # 存放每一次压入数据时，栈中的最小值
                            # （如果压入数据的值大于栈中的最小值就不需要重复压入最小值，
                            # 小于或者等于栈中最小值则需要压入）
    def push(self, x):
        self.stack.append(x)
        if not self.minStack or self.minStack[-1] >= x:
            self.minStack.append(x)

    def pop(self):  # 移除栈顶元素时，判断是否移除栈中最小值
        if self.minStack[-1] == self.stack[-1]:
            del self.minStack[-1]
        self.stack.pop()

    def top(self):   #获取栈顶元素
        return self.stack[-1]

    def getMin(self): 
        out = self.minStack[-1]#获取栈中的最小值，想要O（1）时间实现，可以先存一下
        return out

    def all(self):  #列表栈中所有的元素
        return self.stack[:]

美团面试：栈的压入、弹出序列
输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。（注意：这两个序列的长度是相等的）
思路：
既然是比较找的压入顺序和栈的弹出顺序，因此，我们可以借助一个辅助栈，将压入序列中的元素，依次压入栈中，每压入一个元素，都需要和弹出序列相比较，相同则出栈。以pushV[1,2,3,4,5],popV[4,5,3,2,1]为例。先将第一个元素放入栈中，这里是1，然后判断栈顶元素是不是出栈顺序的第一个元素，这里是4，很显然1≠4，所以我们继续压栈，直到相等以后开始出栈，出栈一个元素，则将出栈顺序向后移动一位，直到不相等，这样循环直到，压栈顺序遍历完成。
理论上说，这样模拟压栈出栈顺序，如果弹出序列是压入序列的一个弹出顺序，那么当弹出序列遍历完成的时候，辅助栈stack应该为空，因为都出栈了，否则，弹出序列不是当前压入序列的一个弹出顺序。

class Solution:
    def IsPopOrder(self, pushV, popV):
        # write code here
        if len(pushV) != len(popV):
            return False
        if pushV == None and popV != None:
            return False
        if pushV != None and popV == None:
            return False
        stack = []    # 构造辅助栈
        index = 0     # 从头开始遍历popV
        for i in range(len(pushV)):
            stack.append(pushV[i])  # pushV依次入栈
            while stack and stack[-1] == popV[index]:  
            # 每一次入栈,栈顶元素都要和出栈顺序比较，直到栈空或不相等
                stack.pop()      # 相等则出栈，再继续popV的下一个元素比较
                index += 1   # 
        if stack:
            return False
        else:
            return True

两数相除：不能实用除号，完成除法的函数编写
位运算方法，因为某进制的移位等于乘除法，比如二进制左移一位等于加上其乘以进制的n次方

def divide(self, dividend, divisor):
        """
        :type dividend: int
        :type divisor: int
        :rtype: int
        """
        flag=1
        if (dividend<0 and divisor>0) or (dividend>0 and divisor<0):flag=-1
        m,n=abs(dividend),abs(divisor)
        res=0
     
        while m>=n:
            p,t=1,n
            while m>= t<<1: #t左移一位，
                p<<=1 #对应p也同时左移，patch+1
                t<<=1
            res+=p
            m-=t
       
        res*=flag
        if res<-2**31 or res>2**31-1:return 2**31-1
        return res

纯加减法：从计数1开始，让除数不断翻倍，得到的计数也翻倍，去逼近被除数，最后得到计数就是商

class Solution(object):
    def divide(self, dividend, divisor):
        """
        :type dividend: int
        :type divisor: int
        :rtype: int
        """
        #官方样例bug
        if dividend == -2147483648 and divisor == -1:
            return 2147483647
        if dividend == 0:return 0
        if divisor == 1:return dividend
        if divisor == -1:return -dividend
        a = dividend
        b = divisor
        sign = 1
        if (a > 0 and b < 0) or (a < 0 and b > 0) :
            sign = -1
        a = abs(a)
        b = abs(b)
        res = self.div(a,b)
        return res*sign
    def div(self,a,b):
        if a < b:return 0
        count = 1
        tb = b #除数不变
        while tb+tb <= a:
            count += count
            tb += tb
        return count + div(a-tb,b) #递归逼近被除数，比如60除以8，第一次，tb会8+8,16+16 ,这个时候conut就1+1,2+2,最后得4，此时对应从div（60-32，8）开始递归，tb 只8+8 count就 1+1等于2 继续从div（28-16,8），此时tb只能是8，所以count = 1，统计起来1+2+4就是7，如果还要求余数就是最后的12-8=4

9.1深信服第一题：日志分析
一组攻击先后包含 s w r。现有 T 份日志，每份是一个小写字母字符串，需要从每份日志里，统计有多少种可能的潜在攻击。
输入：正整数 T，紧接着是 T 行日志
输出：T 行，每个日志的潜在攻击数。需要对 1e9+7 取模

解法：这题相当于查找字符串中有多少个 “swr” 子序列。用动态规划比较高效，否则有些大测试点估计过不了
考虑如下三个动态规划函数：
dp_s。其中 dp_s[i] 代表字符串的前 i 个字符，有多少个子序列 “s”。
dp_sw。其中 dp_sw[i] 代表字符串的前 i 个字符，有多少个子序列 “sw”。
dp_swr。其中 dp_swr[i] 代表字符串的前 i 个字符，有多少个子序列 “swr”。
状态转移，需要看字符串的第 i 位是什么。比如是 ‘r’，那么它可以额外提供的 “swr” 子序列数量即为 dp_sw [i]。其余同理，因此状态转移函数总结如下：
如果字符串的第 i 位是 ‘s’，则 dp_s[i] = dp_s[i - 1] + 1，否则 dp_s[i] = dp_s[i - 1]
如果字符串的第 i 位是 ‘w’，则 dp_sw[i] = dp_sw[i - 1] + dp_s[i]，否则 dp_sw[i] = dp_sw[i - 1]
如果字符串的第 i 位是 ‘r’，则 dp_swr[i] = dp_swr[i - 1] + dp_sw[i]，否则 dp_swr[i] = dp_swr[i - 1]
注意到，每个函数只有最后一个值会被用到，因此可以用滚动数组节省空间。
我只用了 s w r 三个变量表示循环中的三个函数值。最终输出 dp_swr[n] % (1e9+7) 的值即可。

T = int(input())
for _ in range(T):
    info = input()
    s = w = r = 0
    for i in range(len(info)):
        if info[i] == 's':
            s += 1   # 遍历到第i位时，s表示 dp_s[i]的值，下同
        elif info[i] == 'w':
            w += s
        elif info[i] == 'r':
            r += w
    print(int(r % (1e9+7)))

第二题：深信服旅游
有 T 组测试数据。每组包含正整数 n，表示员工数。之后是 n 行，每行两个正整数a, b，表示一位员工方便旅游的时间段为 [a, b]。问最多可以同时让多少位员工觉得方便。
输入：正整数 T。之后 T 组数据，每组先输入正整数 n；然后是 n 行，每行两个正整数
输出：T行，每组测试数据的结果
备注：O(n^2)的算法可得一半分，O(nlogn)的算法可得满分

对于每组数据，分别用数组A， B记下来所有的开始时间和所有的结束时间，并不需要考虑它们来自于哪位员工。将它们升序排列。
为什么不需要考虑它们来自哪个员工呢？
因为我们只关注每个区间的进入和退出。比如两个区间 (1,4)+(2,3)，实际上和 (1,3)+(2,4) 是没有区别的。
我们要做的，是给定这些区间的首尾值，判断最多有多少个区间重合。
遍历数组A，每次找到 A[i]，相当于有一个区间开始。我们还要查看这时有多少区间已经结束。因此需要在数组B中维护一个动态指针p（p表示当前有多少个区间已经结束）。如果当前p指向的结束时间小于 A[i]，说明当前的区间已经结束，需要不断将p右移。操作完成后， p 和 i 的下标差加1即为当前区间的重合数。
最后，每步中找到的区间重合数去一个最大值即为所求。

T = int(input())
for _ in range(T):   #  T组测试数据
    n = int(input())
    A, B = [], []
    for __ in range(n):     # 每组数据n个员工
        a, b = [int(x) for x in input().split()]
        A.append(a)
        B.append(b)
    A.sort()
    B.sort()
    p = ans = 0
    for i in range(n):
        while p < n and A[i] > B[p]:
            p += 1
        ans = max(ans, i - p + 1)
    print(ans)

17.第三题：五进制
设定一种五进制，其中 o, y, e, a, s 分别代表 0, 1, 2, 3, 4。例如五进制 ya 代表十进制 8。
有 T 组测试数据。每组包含一个数字，或字母oyeas组成的字符串。实现进制的相互转换，并输出每个测试数据的转换结果。
输入：正整数 T。之后 T 行，每行一个【五进制字母串】或【十进制数】
输出： T 行，给定测试如果是五进制，则输出十进制数；给定测试如果是十进制，则输出五进制字符串

压轴题反而是最简单的，跟二进制转化没啥区别。
十进制转五进制，每次对5取模，得到最低位，然后将数字除以5，直到数字变为零；
五进制转十进制，遍历字符串。长度为 n 的字符串，第 i 位是x，则它的贡献为 x * 5 ^ (n - i - 1)。循环求和即可

import math
T = int(input())
for _ in range(T):
    ipt = input()
    if ipt.isdigit():
        if ipt == '0':
            print('o')
            continue
        ans = ''
        ipt = int(ipt)
        while ipt > 0:
            ans = 'oyeas'[ipt % 5] + ans
            ipt //= 5
        print(ans)
    else:
        ans = 0
        for i in range(len(ipt)):
            ans += 'oyeas'.index(ipt[i]) * math.pow(5, len(ipt) - i - 1)
        print(int(ans))

No Game No Coding

无游戏不编程

Leetcode学习日历

数据结构基础

算法性能：时间复杂度与空间复杂度

数组

二分查找问题

元素移除问题

有序数组的平方问题

长度最小的子数组问题

螺旋矩阵问题

轮转数组/旋转链表/翻转字符串里的单词

数组[列表]排序问题:手撕排序

数组部分总结

链表

什么是链表？

移除节点

设计链表

翻转链表

两两节点交换

删除链表的倒数N节点（三次AC）

链表相交

环形链表II

哈希表 （key:value/O1时间访问）

有效字母异位词

两个数组的交集

快乐数

三数之和

多位数的和与加

赎金信问题

字符串

反转字符串

替换空格

比较字符串的大小

翻转字符串中的单词

左旋转字符

实现sreStr()

重复的子字符串

无重复最长子串（三次AC）

字符中的最长回文子串

数据结构：栈、堆、队列

有效括号问题

碰碰消：删除字符串中所有的相邻重复游戏

二叉树/递归

二叉树的遍历（遍历问题学习递归，迭代的思想）

二叉树的属性

方法总结

二叉树的修改与构造

解题思路

求二叉搜索树的属性

公共祖先问题

二叉树的修改与构造

解题思路总结

常见算法

贪心算法

什么是贪心

分发饼干问题

摆动序列问题：独立做出来的第一道中等题

最大子序列和

经典问题:股票买卖获得的最大收益

回溯算法

组合问题

分割回文串问题

子集问题

动态规划

什么是DP（动态规划）

解题步骤（动规五部曲）

DP如何debug

背包问题

打家劫舍

股票问题

子序列问题

深度优先搜索算法DFS

广度优先搜索算法BFS

刷题总结，代码随想录就是一个刷题套路集合

以后的纯刷题部分

哈希表（key:value/O1时间访问）